HASH GAME - Online Skill Game GET 300

　　上讲的主要内容 公钥密码体制的简介 基于RSA的公钥密码算法 数字证书的简介 公钥密码体制的优缺点 1 第四讲Hash 函数及应用 主讲人：谷利泽 Email ：Tel: 010 本讲的要点 掌握Hash 函数的性质 了解SHA-1算法的实现过程 理解数字签名的基本思想 理解消息认证的基本思想 3 引言 在一个开放通信网络的环境中，信息面临的攻击包括窃 听、伪造、修改、插入、删除、否认等。因此，需要提供用 来验证消息完整性的一种机制或服务消息认证。这种服务 的主要功能包括： 确保收到的消息确实和发送的一样； 确保消息的来源真实有效； 注：对称密码体制和公钥密码体制都可提供这种服务，但用于 消息认证的最常见的密码技术是基于哈希函数的消息认证码。 4 认证码和检错码 现代密码学中的消息认证码与通信学的消息检错 码有密切的联系，并由其演变而来。 检错码是检测由于通信的缺陷而导致消息发生错误的 方法； 认证码是用来检查因恶意或有目的等而致使消息发生 变化的技术。 5 哈希（Hash）函数的简介 也称散列函数、杂凑函数等，是一种单向密码体制，即 它是一个从明文到密文的不可逆映射，即只有加密过程，不 存在解密过程。同时，Hash函数可以将“任意”长度的输 入经过变换以后得到固定长度的输出。 Hash函数的这种单 向特征和输出数据长度固定的特征使得它可以生成消息或数 据块的“数据指纹”(也称消息摘要或散列值)，因此在数据 完整性和数字签名等领域有广泛的应用的，哈希函数在现代 密码学中起着重要作用。 6 哈希函数的表示 对不同长度的输入消息，产生固定长度的输出。这个 固定长度的输出称为原输入消息的“散列”或“消息摘要” (Message Digest)。 公式表示形式： h=H(M) M ：任意长度的消息 H ：哈希(Hash)函数或杂凑函数或散列函数 h：固定长度的哈希值 7 哈希算法的性质(特点) 输入：消息，任意有限长度。 输出：哈希值，固定长度。 容易计算：对干任意给定的消息，容易计算其哈希值。 单向性：对于给定的哈希值h，要找到M使得H(M)＝h在计 算上是不可行的。 8 哈希算法的性质(安全性) 抗弱碰撞性：对于给定的消息M ，要发现另一个消息M ， 1 2 满足H(M )＝H(M )在计算上是不可行的。 1 2 抗强碰撞性：找任意一对不同的消息M M ，使H(M )＝ 1， 2 1 H(M )在计算上是不可行的。 2 雪崩效应：当一个输入位发生变化时，输出位将有一半会 发生变化。 9 哈希函数的一般结构 输入分组 输入分组的长度 分组数 M0 M1 ML-1 b b b n n f n f n „ n f IV =CV0 CV1 CVL- 1 初始值 链接变量 压缩函数 哈希值长度 10 哈希函数的核心技术 设计无碰撞的压缩函数f，而攻击者对算法的攻击重点 是压缩函数f 的内部结构，由于压缩函数f 和分组密码一样 是由若干轮处理过程组成，所以对压缩函数f 的攻击需通过 对各轮之间的位模式的分析来进行，分析过程常常需要先找 出压缩函数f 的碰撞。由于是压缩函数，其碰撞是不可避免 的。因此，在设计压缩函数f 时就应保证找出其碰撞在计算 上是不可行的。 常用的散列函数： MD5； SHA系列； 11 SHA的简介 美国国家标准技术研究所NIST于1993年开发的另一个 散列算法称为SHA。两年之后，这个算法被修改为了今天广 泛使用的形式。修改后的版本是SHA-1，是数字签名标准中 要求使用的算法。 SHA接受任何有限长度的输入消息，并产生长度为160 比特的Hash值（MD5仅仅生成128位的摘要），因此抗穷举 性更好。SHA-1 设计时基于和MD4相同原理，它有5个参与 运算的32位寄存器字，消息分组和填充方式与MD5相同，主 循环也同样是4轮，但每轮进行20次操作，非线性运算、移 位和加法运算也与MD5类似，但非线性函数、加法常数和循 环左移操作的设计有一些区别。 12 SHA-1的结构 消息Ｍ 填充使分组恰好512位 M M „ M 1 2 t 初 哈 始 f f „ f 希 值 值 13 SHA-1哈希值的生成过程 L512 bits N bits 填充(0to 511 bits) 消 息 100…0 消息长度L (mod 264) 512 bits 512 bits 512 bits 512 bits M0 M1 „ Mi „ ML-1 512 512 512 512 160 160 160 160 160 IV HSHA-1 HSHA-1 „ HSHA-1 „ HSHA-1 CV1 CVi CVL-1 哈希值 14 SHA-1对单个512位分组的处理过程 M 512比特 hi-1(160比特) i 初始值： A=0 A B C D E B=0xefcdab89 f , K , W[0…19] 20步 C=0x98badcfe 1 t D=0 A B C D E E=0xc3d2e1f0 f , K , W[20…39] 20步 2 t A B C D E f , K , W[40…59] 20步 3 t A B C D E f , K , W[60…79] 20步 4 t + + + + + 模232加 h (160比特) i 15 SHA-1生成字W 的方法 t 1 W =S (W +W +W +W ) (t=16,17,…,79) t t-16 t-14 t-8 t-3 M (512bit) w ,w ,w ,w „ w ,w ,w ,w „ w ,w ,w ,w i 0 2 3 8 t-16 t-14 t-8 t-3 63 65 71 76 + 循环左 + + 移一位 S1 S1 S1 W W0 „ W15 W16 „ Wt „ 79 16 SHA-1的基本操作 5 A=E+ft (B,C,D)+S (A)+W +K ; f (X, Y, Z) = (X∧Y) ∨(～X ∧Z) (t=0,…,19) t t t B=A; f (X, Y, Z) = X ⊕Y ⊕Z (t=20,…,39) t C=S30(B); f (X, Y, Z) =(X∧Y) ∨(X∧Z) ∨(Y∧Z) (t=40,…,59) t f (X, Y, Z) = X ⊕Y ⊕Z (t=60,…,79) D=C; t E=D; A B C D E K 的4个取值2 、3、5 、10的 t 平方根，然后再乘以230 ，最 后取结果的整数部分。 f + S5 + S30 + Wt + Kt K =0x5a827999 (t=0,…,19) t K =0x6ed9ebal (t=20,…,39) t K =0x8f1bbcdc (t=40,…,59) A B C D E t K =0xca62c1d6 (t=60,…,79) t 17 哈希函数的应用 数字签名 消息认证 譬如可信计算、文件病毒 的检验、网页防篡改、黑 口令的安全性 白名单等许多应用。 文件的完整性 譬如零知识证明、比特承 密码协议的应用 诺、投掷硬币、电子商务 的安全协议等许多应用。 18 数字签名的简介 数字签名体制是以电子签名形式存储消息的方法，所签 名的消息能够在通信网络中传输。 在当今数字化的信息世界里，数字化文档的认证性、完 整性和不可否认性是实现信息化的基本要求，也决定信息 化的普及和推广。数字签名是满足上述要求的主要手段之 一，也是现代密码学的主要研究内容之一。 数字签名是日常生活中手写签名的电子对应物。 19 数字签名与手写签名的不同 签名：手写签名是被签文件的物理组成部分；数字签名是 连接到被签消息上的数字串。 传输方式：数字签名和所签名的消息能够在通信网络中传 输。手写签名使用传统的安全方式传输。 验证：手写签名是通过将它与真实的签名进行比较来验证； 而数字签名是利用已经公开的验证算法来验证。 数字签名的复制是有效的；而手写签名的复制品是无效的。 手书签字是模拟的，且因人而异。数字签字是0和1的数字 串，因消息而异。 20 数字签名的含义 所谓数字签名（Digital Signature），也称电子签 名，是指附加在某一电子文档中的一组特定的符号或代码， 它是利用数学方法和密码算法对该电子文档进行关键信息 提取并进行加密而形成的，用于标识签发者的身份以及签 发者对电子文档的认可，并能被接收者用来验证该电子文 档在传输过程中是否被篡改或伪造。 21 数字签名的安全要求 签名是可以被验证的； 接受者能够核实签名者对消息的签名。 签名是不可伪造的； 除了签名者，任何人（包括接受者）不能伪造消息的签名。 签名是不可重用的； 同一消息不同时刻其签名是有区别的。 签名是不可抵赖的； 签名者事后不能抵赖对消息的签名，出现争议时，第三方可解 决争端； 22 数字签名方案的组成 数字签名方案是由五元组组成的， 即{P,S,K,Sig,Ver} 。 P:明文空间； S:签名空间； K:密钥空间； Sign:签名算法； Ver:验证算法； 23 数字签名的过程 系统初始化过程： 生成数字签名方案用到的所有参数。 签名生成过程 用户利用给定的算法对消息产生签名s=Sign(m)。 签名验证过程 验证者利用公开的验证方法对给定消息的签名进行 验证，得出签名的有效性。Ver(s,m)=0或1。 24 数字签名的基本原理 签名者A 验证者B 消息 Hash函数 哈希值 Hash函数 消息 签名有效 消息 公开信道 验证算法 哈希值 签名 签名 签名无效 签名算法 A的公钥 A的私钥 25 RSA数字签名方案(初始化) 1。选取两个大素数p和q，两个数长度接近，1024位 2 。计算n=p*q,

　　(n)=(p-1)(q-1) 3. 随机选取整数e(1e

　　(n))，满足gcd(e,

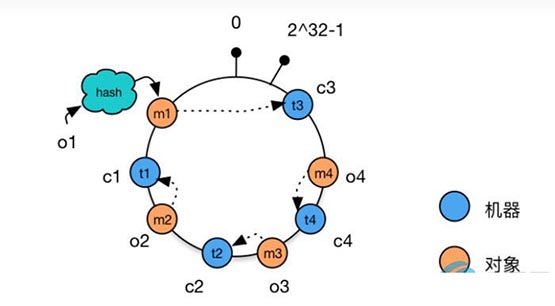
　　(n))=1 4.计算d，满足d*e=1 （mod

　　(n)）。 注：n公开，p和q保密。 e为公钥，d为私钥。 26 RSA数字签名方案(签名和验证) 签名算法 1.利用一个安全的Hash函数h来产生消息摘要h(m)。 2.用签名算法计算签名s=Sig (m)=h(m)d mod n。 k 验证算法 1.首先利用一个安全的Hash函数h计算消息摘要h(m)。 2.用检验等式h(m) mod n=se mod n 是否成立，若相等签 名有效，否则，签名无效。 27 RSA数字签名方案(正确性) 由于 s=h(m)d mod n d*e=1 （mod

　　(n)） 所以 se mod n=h(m)ed mod n =h(m) k

　　(n)+1 mod n = h(m) *h(m) k

　　(n) mod n

　　(n) k =h(m)* (h(m) ) mod n = h(m) 28 RSA数字签名方案(举例) 初始化： 假设A选取p = 13，q = 11，e = 13，则有n = pq = 143，φ(n) = (p- 1)(q-1) = 12×10 = 120。求解ed = 13d ≡ 1(mod 120) 得d = 37。因此 A 的公钥为 （n = 143,e = 13）；私钥为d = 37。 签名过程： 假定消息m的Hash值h(m) = 16，则计算m签名s = h(m)d mod n = 1637 mod 143 = 3。 验证过程： 接受者B收到签名后，计算se mod n = 313 mod 143 = 16，h(m) mod e n = 16 mod 143 = 16，等式h(m) mod n = s mod n成立，因此，B验 证此签名有效。 29 哈希函数的应用 数字签名 消息认证 口令的安全性 文件的完整性 密码协议的应用 30 消息认证的概述 网络系统安全一般要考虑两个方面：一方面，加密保 护传送的信息，使其可以抵抗被动攻击；另一方面，就是 要能防止对手对系统进行主动攻击，如伪造、篡改信息等。 认证是对抗主动攻击的主要手段，它对于开放的网络中的 各种信息系统的安全性有重要作用。 认证可分为实体认证和消息认证。